
For example when I try $\int \arctan x \space dx$ I get a mess that doesn't appear to work (but maybe it does and I just don't see how). I would also like to know if there are problems for which this method cannot work.When you realize the u column will never hit zero, when do you stop? From what I can read it seems you stop once you try differentiating twice.It took me a while to type all this so I thought I'd still go ahead and post it.
#Tabular method full
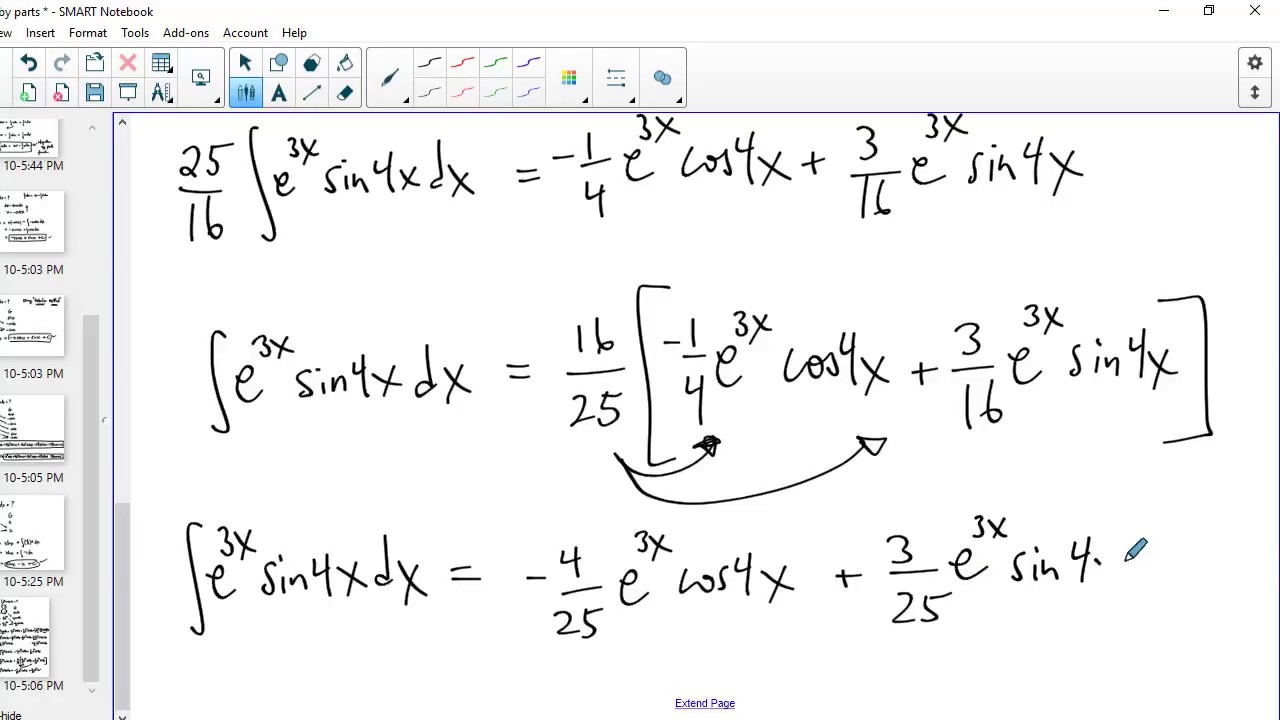
I started writing this question thinking that $\int ln(x)\space dx $ can't be solved with the Table Method, but in the process of composing this question it appears it can be in a similar way $\int e^x \cos x \space dx$ can be solved (at least with regards the handling of the last full row going across as an integral instead of diagonal as a non-integral). The College Mathematics Journal, September 1990, Volume 21. This then works out to $x \ln x - x + C$, which is the correct answer. David Horowitz, Golden West College, Huntington Beach, CA 92647. But I find it doesn't seem to work at all on some problems (maybe I'm wrong?).įor example, consider: $\int ln(x)\space dx $ (I realize this is an easy one, but I wanted to try the Table Method on it). Subject classification(s): Calculus Single Variable Calculus Integration Applicable Course(s): 3.2 Mainstream Calculus II. How would you fill in the rows and columns in the table below How might we reverse the tabular method for multiplying polynomials to solve a polynomial. It incorporates the same substitutions that are used for integration by parts, but you create a table of repeated derivatives and antiderivatives of the substitutions to find the solution. This is a systematic step by step procedure for minimizing a Boolean expression in standard. I really find this method appealing because it looks easier and quicker on many problems. Tabular integration, also called the DI method, is a way to integrate a function by repeatedly differentiating and integrating parts of it. The Quine-McCluskey or Tabular method is employed in such cases.
In a supplemental book I have it brings up something called the Table Method.

I'm learning about integration by parts, primarily from Stewart's text (7th edition).


 0 kommentar(er)
0 kommentar(er)
